オブジェクトが動く速度と加速度と微分の考え方 [Edit]
投稿者：野中 文雄 | 投稿日：2014.03.17 | [CreateJS][HTML5][野中ゼミ]物理法則にしたがったオブジェクトのアニメーションをスクリプティングするとき、数学の「微分」の考え方で捉えられると応用の幅が広がります。微分と聞くと難しそうに響きます。けれど、大雑把にいってしまえば、オブジェクトの動きについて変化を見るということです。アニメーションがつぎのフレームでどう変わるかを考える、といってもよいでしょう。
01 等速直線運動
決まった速さで同じ向きに動き続ける「等速直線運動」なら、つぎのフレームに移るたびにオブジェクトの位置(xy座標)に定数を足します。この定数(xy平面で捉えるならベクトル)が速度です。つぎのフレームにおけるオブジェクトの位置は、今の位置に速度を加えて求めます。
位置 += 速度
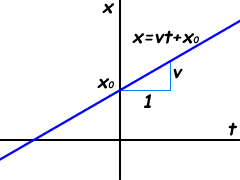
時間(t)と位置(x)をそれぞれ横軸と縦軸にした等速直線運動のグラフは、下図001のように一次関数(x = vt + x0)で表されます(「直線の式(方程式)」参照)。一次関数は微分すると、直線の傾きを示す定数になります(x' = v)。そして、この定数値(v)が等速直線運動の速度です。
x = vt + x0
x' = v
図001■等速直線運動の位置は時間の一次関数で表される
02 等速円運動の位置と速度
等速円運動は、円周上を決まった速さで回ります。ただし、一定なのは時間あたりの回転角(角速度)です。運動の向きは円の接線と一致しますので、時間とともに変わります。その場合、速度も時々刻々と変化することになるのです。
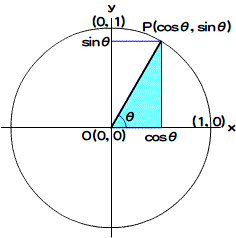
半径1の円周(「単位円」といいます)上でx軸の正方向となす角度がθの点(P)の座標は、三角関数で(cosθ, sinθ)と定められています(図002)。すると、等速円運動の位置(x, y)は、円軌道の半径(r)と時間(t)あたりの角速度(ω)により、つぎの式で示されます。この方程式は、時間(t)から直に位置(x, y)を導いています。
x = r cos(ωt)
y = r sin(ωt)
図002■単位円の円周上の座標は原点と結ぶ線分がx軸となす角をθとするとき(cosθ, sinθ)
位置の変化を微分すれば速度です。上記の方程式を微分すると、等速円運動の速度がつぎのように導けます(「等速円運動を三角関数の微分で表す」参照)。前述01「等速直線運動」と違って、ことさら簡単な式にはなりません。けれど、位置に速度を加えれば、つぎのフレームにおけるオブジェクトの位置が決まるのは同じです。
x' = -rω sin(ωt)
y' = rω cos(ωt)
この速度を位置に加えて円運動させると、円軌道の中心がどこかは気にせずにスクリプティングできます。詳しくは、「等速円運動を三角関数の微分で表す」をお読みください。つぎのサンプル001が、CreateJSを用いた応用例です。
サンプル001■EaselJS 0.7.1: Particles
03 速度の微分が加速度
位置の変化の微分が速度でした。その速度の変化をさらに微分すると加速度が導かれます。アニメーションでもっともよく使われる加速度は重力(「重力加速度」)でしょう。重力は定数として捉えられます。そして、速度にフレームあたりの重力(加速度)を加えると、つぎのフレームの速度が得られます。その速度をさらに位置に加えれば、放物線運動するオブジェクトのつぎのフレームにおける位置が求まります。
速度 += 加速度
位置 += 速度
もっとも、フレームあたりの速度や加速度というのは、値を1フレームにかかる時間の平均(平均速度と平均加速度)で捉えることになります。厳密には、微分は瞬間の値を定める関数です。けれど、1フレームの時間が十分小さければ、平均でも近似値として扱えます。
さて、この考え方にもとづいて、バネの動きを加速度から定めることができます。バネ運動も前述02「等速円運動の位置と速度」と同じく、一般には三角関数で表されます。したがって、速度や加速度を微分で求めても、簡単な式にはなりません。
けれど、バネ運動は釣合った点(均衡点)から離れるほど、もとの位置に戻ろうとする力が強くなります。バネの引戻す力というのは、重力と同じく加速度です。つまり、バネの加速度は均衡点に向けて、均衡点からの距離に比例した大きさになります。
加速度 = (均衡点 - 位置)×比例係数
速度 += 加速度
位置 += 速度
この式を使えば、三角関数どころか、簡単な四則演算だけでバネ運動が表せるのです。詳しくは「バネのような動きを加速度から定める ー オイラー法」をお読みください。つぎのサンプル002が、CreateJSを用いた応用例です。
サンプル002■EaselJS 0.7.1: Smooth Line tuned
