[AS3] 三角関数で座標を回転するふたつの計算方法

[AS3] 三角関数で座標を回転するふたつの計算方法 [Edit]

投稿者：野中文雄 | 投稿日：2011.09.22 | [AS 3][ActionScript][Tips][野中ゼミ]

角度からxy座標を定めるには、三角関数が用いられます。具体的には、つぎのふたつの計算の仕方があります。これらふたつの違いと使い方をご紹介します。

【角度からxy座標を定める】

原点からの距離がrで正のx軸となす角度がθの座標

x座標: r cosθ
y座標: r sinθ

座標(x, y)を原点でθ回転した座標

x座標: x cosθ - y sinθ
y座標: x sinθ + y cosθ

01 原点からの距離と角度で位置を定める

三角関数は、原点(0, 0)からの距離が1で正のx軸となす角度がθのxy座標を(cosθ, sinθ)と定めました(gihyo.jp連載「ActionScript 3.0で始めるオブジェクト指向スクリプティング」第16回「三角関数を使った楕円軌道のアニメーション」参照)。したがって、原点からの距離がrで正のx軸となす角度がθのxy座標は(r cosθ, r sinθ)になります(図001)。

x = r cosθ
y = r sinθ

図001■原点からの距離がrで正のx軸となす角度がθの座標をsinとcosで表す

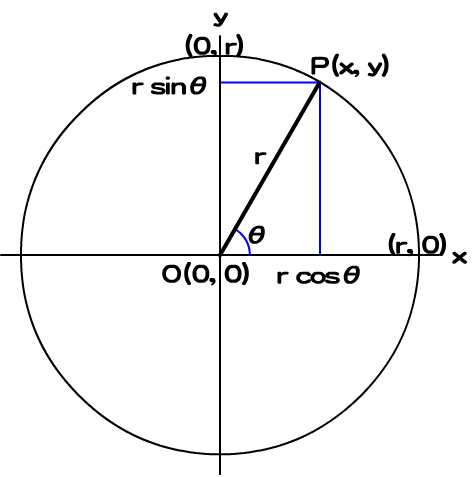
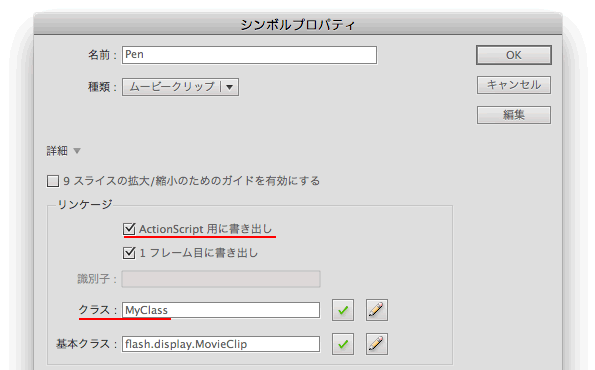
原点を中心とした座標の回転は、上式で角度θを増減させればよいことになります。MovieClipインスタンスをタイムラインに動的に置いて、ステージの真ん中を軸に回してみましょう。まずは、[ライブラリ]でMovieClipシンボルを選び、[シンボルプロパティ]ダイアログボックスで[ActionScript用に書き出し]にチェックして、[クラス]にはMyClassと入力します(図002)。

図002■ MovieClipシンボルにクラスを設定する

以下のスクリプト001をメインタイムラインのフレームに書くと、動的につくられたMovieClipインスタンス(my_mc)がステージ中央を原点として回ります(図003)。予め親Spriteインスタンス(mySprite)を置いて、原点となる基準点をステージの真ん中にしました。

MovieClipインスタンス(my_mc)は、角度0となる時計の3時の位置からアニメーションを始め、DisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)のリスナー関数(xRotate())が三角関数sinとcosによりインスタンスの座標を回しています(スクリプト001)。

スクリプト001■ インスタンスの原点からの距離と角度を定めて回す

var radius:Number = 50;
var radians:Number = 0;
var theta:Number = 0.05;
var mySprite:Sprite = new Sprite();
var my_mc:MovieClip = new MyClass();
addChild(mySprite);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
mySprite.addChild(my_mc);
my_mc.x = radius;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
	radians +=  theta;
	my_mc.x = radius * Math.cos(radians);
	my_mc.y = radius * Math.sin(radians);
}

02 座標を原点から一定の角度回す

2次元平面の座標(x, y)を原点で角度θ回転した点(x', y')は、つぎの式で表されます。原点からの距離や正のx軸となす角度を調べることなく、平面上のどこにある座標でも決まった角度回した位置が求められます。

x' = x cosθ - y sinθ
y' = x sinθ + y cosθ

前掲スクリプト001のインスタンスを回転するアニメーションは、この式で定めるならつぎのスクリプト002のようになります。インスタンスの原点からの距離や正のx軸となす角度は、予め知る必要がありません。

スクリプト002■インスタンスのxy座標を直接変換して回す

var radius:Number = 50;
var theta:Number = 0.05;
var nSin:Number = Math.sin(theta);
var nCos:Number = Math.cos(theta);
var mySprite:Sprite = new Sprite();
var my_mc:MovieClip = new MyClass();
addChild(mySprite);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
mySprite.addChild(my_mc);
my_mc.x = radius;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
	var nX:Number = my_mc.x;
	var nY:Number = my_mc.y;
	my_mc.x = nCos * nX - nSin * nY;
	my_mc.y = nSin * nX + nCos * nY;
}

03 ふたつの計算の使い方

前掲スクリプト001と002はひとつのインスタンスを回すだけですので、それのみではどちらがよいとはいいきれません。原点からの距離および正のx軸となす角度が定まっていれば、前述01「原点からの距離と角度で位置を定める」の式によるのが定石でしょう。

けれど、距離や角度は調べなければわからないとき、あるいは多くの座標を同じ角度回すときには前項02「座標を原点から一定の角度回す」の式がスマートです。xy座標だけがわかればよく、しかも回す角度が決まっていれば三角関数の値も定数扱いできるからです。

つぎのスクリプト003は、100個のMovieClipインスタンスんをVectorオブジェクト(MovieClipベース型)に納めて、02の式ですべて同じ角度ずつ回します(図003)。

図003■100個のインスタンスを同じ角度ずつ回す

スクリプト003■数多くのインスタンスのxy座標を直接変換して回す

var count:uint = 100;
var maxRadius:Number = 70;
var theta:Number = 0.05;
var nSin:Number = Math.sin(theta);
var nCos:Number = Math.cos(theta);
var mySprite:Sprite = new Sprite();
var instances:Vector.<MovieClip> = new Vector.<MovieClip>(count);
addChild(mySprite);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
for (var i:uint = 0; i < count; i++) {
	var radius:Number = maxRadius * Math.random();
	var radians:Number = 2 * Math.PI * Math.random();
	var my_mc:MovieClip = new MyClass();
	mySprite.addChild(my_mc);
	my_mc.x = radius * Math.cos(radians);
	my_mc.y = radius * Math.sin(radians);
	instances[i] = my_mc;
}
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
	for (var i:uint = 0; i < count; i++) {
		var my_mc:MovieClip = instances[i];
		var nX:Number = my_mc.x;
		var nY:Number = my_mc.y;
		my_mc.x = nCos * nX - nSin * nY;
		my_mc.y = nSin * nX + nCos * nY;
	}
}

リスナー関数(xRotate())がすべてのインスタンスを回す計算に用いるsinとcosの値は予め変数(nSinおよびnCos)に入れられていて、メソッドMath.sin()もMath.cos()も呼出されていないことにご注目ください。メソッドの呼出しがなければ、その分演算は速くなります。

なお、初めにforループで各インスタンスの位置をランダムに決めるときには、01の式を使いました。

もちろん、インスタンスの原点からの距離および正のx軸となす角度は計算で導けます。前者は三平方の定理、後者にはMath.atan2()メソッドを使います。たとえば、インスタンス(my_mc)の距離(radius)と角度(radians)はつぎのスクリプトで求められます。

var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
var radius:Number = Math.sqrt(nX * nX + nY * nY);
var radians:Number = Math.atan2(nY, nX);

しかしこのやり方では、リスナー関数(xRotate())が呼出されるたびに、すべてのインスタンスについていちいち計算しなければなりません^[*1]。それに、01の式で座標を定めるときも、三角関数sinとcosの値がインスタンスごとに毎回変わります。スクリプト003の方が優れているといえるでしょう。

ふたつのやり方で計算したそれぞれの速さを、wonderflのコードで比べてみました。polarが式01、transformが式02になります。

Calculating coordinates to rotate - wonderfl build flash online

[*1] Vectorオブジェクトにインスタンスごとの距離と角度を納めておけば、いちいち計算する手間はなくなります。けれど、スクリプト003であればそれらの値そのものが必要ありません。

F-site