[AS3] 3次元回転の軸をベクトルの外積で求める

[AS3] 3次元回転の軸をベクトルの外積で求める [Edit]

投稿者：野中文雄 | 投稿日：2011.01.22 | [AS 3][ActionScript][Tips][野中ゼミ]

3次元空間のオブジェクトをマウスポインタの位置に応じて回すときの考え方です(図001)。Matrix3Dクラスで座標変換する場合、水平方向と垂直方向それぞれについて回転を加える方法がひとつあります。今回はもうひとつのやり方として、水平・垂直合わせてベクトルの外積により回転軸を求めてみます。

図001■四方に置いた面を上下左右に回す

矩形の画像で四方を囲み、上下左右に回す例は、gihyo.jp連載「ActionScript 3.0で始めるオブジェクト指向スクリプティング」第38回「z座標値に応じて重ね順を変える」で解説しました。Matrix3D.appendRotation()メソッドを用いて、水平と垂直それぞれの回転を加える前者の考え方にしたがっています。このサンプル(スクリプト2)に手を加えて、ベクトルの外積から求めた軸で回してみましょう。

手直しするのは、マウスポインタの位置に応じてMatrix3Dオブジェクトに回転を加え、インスタンスのプロパティDisplayObject.transformにTransform.matrix3Dとして設定しているつぎのリスナー関数(スクリプト001)です。なお、このリスナー関数を含めたフレームアクション全体については、前掲解説をお読みください。

スクリプト001■マウスポインタの位置に応じて回転を加えるリスナー関数

function xRotate(eventObject:Event):void {
	var nRotationY:Number = (mouseX - nX) * nDeceleration;
	var nRotationX:Number = (mouseY - nY) * nDeceleration;
	myMatrix3D.appendTranslation(-nX, -nY, 0);
	myMatrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS);  // x座標に応じてy軸(zx平面に垂直な軸)で回す
	myMatrix3D.appendRotation(nRotationX, Vector3D.X_AXIS);  // y座標に応じてx軸(yz平面に垂直な軸)で回す
	myMatrix3D.appendTranslation(nX, nY, 0);
	xSetOrder();
}

Matrix3D.appendRotation()メソッドで回転を加えているのは2行のステートメントです。まず、マウスポインタのx座標の位置に応じてy軸で回します。つぎに、マウスポインタのy座標の位置に応じてx軸で回しています。いい換えると、前者はzx平面に垂直な軸で回し、後者はyz平面に垂直な軸で回すということです。

さらに、マウスポインタの座標を、原点とその座標を結ぶベクトルつまり「位置ベクトル」と捉えてみましょう。すると、どちらも位置ベクトルとz軸から成る平面に垂直な軸で回しているといえます。そうであれば、水平と垂直を分けなくても、マウスポインタの(x, y)座標の位置ベクトルとz軸から成る平面に垂直な軸で回せば同じ結果になるのではないかと予想できます。

z軸もベクトルです。そして、ふたつのベクトルから成る平面に垂直なベクトルは、ふたつのベクトルの外積として導かれます。よって、z軸とマウスポインタの(x, y)座標のふたつのベクトルから外積を求め、それをMatrix3D.appendRotation()メソッドの回転軸(第2引数)として渡すことにします。この考え方で書替えたのがつぎのスクリプト002です(図002)。

スクリプト002■マウスポインタの位置から軸を求めて回転するリスナー関数

function xRotate(eventObject:Event):void {
	var nMouseX:Number = mouseX - nX;
	var nMouseY:Number = mouseY - nY;
	var mouseVector3D:Vector3D = new Vector3D(nMouseX, -nMouseY, 0);
	// z軸とマウス座標の位置ベクトルとの外積を求める
	var axisVector3D:Vector3D = Vector3D.Z_AXIS.crossProduct(mouseVector3D);
	axisVector3D.normalize();
	myMatrix3D.appendTranslation(-nX, -nY, 0);
	// z軸とマウス座標の位置ベクトルが成す平面に垂直な軸で回す
	myMatrix3D.appendRotation(mouseVector3D.length * nDeceleration, axisVector3D);
	myMatrix3D.appendTranslation(nX, nY, 0);
	xSetOrder();
}

図002■ベクトルの外積から求めた軸で回転するように書替えたリスナー関数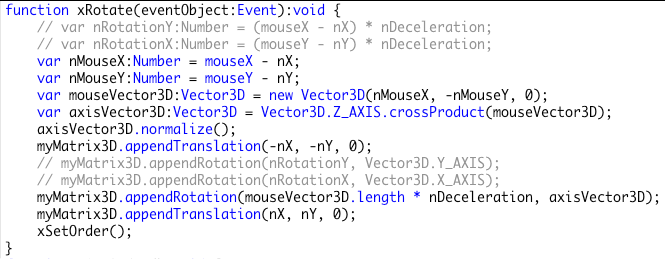

ベクトルの外積は、 Vector3D.crossProduct()メソッドで求められます。ふたつのVector3Dオブジェクトのひとつを参照し、もうひとつは引数に渡します。その順序によって、外積として得られるVector3Dオブジェクトの向きが逆になりますので、ご注意ください。

また、Matrix3D.appendRotation()メソッドの第2引数に渡す回転軸のVector3Dオブジェクトは、長さが1の「単位ベクトル」にします。単位ベクトルに変換するメソッドは、Vector3D.normalize()です。なお、回転する角度は、マウス座標の位置ベクトルの長さ(Vector3D.lengthプロパティ)に比例させました。

これで、Matrix3D.appendRotation()メソッドの呼出しは1度で済みます(前掲スクリプト002)。[ムービープレビュー]を確かめると、もとのスクリプト001と基本的に同じ動きになっているでしょう(前掲図001)。

F-site

[AS3] 3次元回転の軸をベクトルの外積で求める [Edit]