[AS3] Vector3Dの四元数表現

[AS3] Vector3Dの四元数表現 [Edit]

投稿者：野中文雄 | 投稿日：2010.04.02 | [AS 3][ActionScript][Tips][バグ][野中ゼミ]

[ヘルプ]の[Vector3D]クラスで「Vector3D.wプロパティ」の項を読むと、つぎのようなくだりがあります。しかし、これは四元数についての説明ではなさそうです。

四元数表記では、3次元回転の計算の4番目のエレメントとして角度が使用されます。wプロパティを使用すると、Vector3Dオブジェクトの回転角度を定義できます。回転角度と座標(x, y, z)の組み合わせにより、表示オブジェクトの方向が決まります。

Matrix3D.decompose()またはMatrix3D.recompose()メソッドは、その引数として方向スタイルが指定できます。この引数に定数Orientation3D.AXIS_ANGLEを渡すと、Vector3Dインスタンスで受渡しする回転の情報の形式に軸角度が指定されます。すると、回転のVecor3Dインスタンスには、回転軸となる単位ベクトルとラジアン角の値が納められることになります。

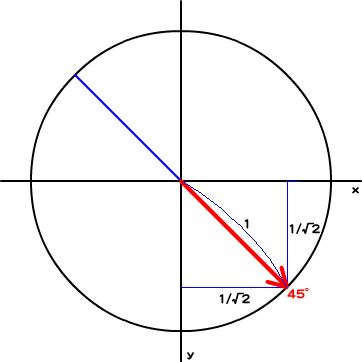
たとえば、x軸に対して45度の角度となる単位ベクトル(1/√2, 1/√2, 0)を回転の軸として(図001)、180度(πラジアン)回転するフレームアクションを試してみましょう(スクリプト001)。

図001■単位ベクトルで回転軸を指定する

スクリプト001■単位ベクトルを軸に回転して軸角度の情報を得る

var myMatrix3D:Matrix3D = new Matrix3D();
var axis:Vector3D = new Vector3D(Math.SQRT1_2, Math.SQRT1_2,0);
myMatrix3D.prependRotation(180, axis);
var axisAngle:Vector3D = myMatrix3D.decompose(Orientation3D.AXIS_ANGLE)[1];
trace(axisAngle, axisAngle.w);

上記スクリプト001は、Matrix3D.decompose()メソッドの第1引数に方向スタイルとして定数Orientation3D.AXIS_ANGLEを指定しました。よって、つぎの[出力]のとおり、回転の情報をもつVector3Dオブジェクト(戻り値のVectorのエレメント1)から回転軸の3次元ベクトルと回転角のラジアン値が得られます。

Vector3D(0.7071067094802856, 0.7071068286895752, -2.339619844353034e-24) 3.1415927410125732

0.707…は1/√2(定数Math.SQRT1_2)、-2.33…e-24はかぎりなく0に近い値、3.14…はもちろんπを表します。したがって、この[出力]が意味するのは、まさに回転軸が(1/√2, 1/√2, 0)で回転角がπラジアン(= 180度)という情報です。

Vector3D.wプロパティは「回転角度」を示し、回転軸を表す3次元ベクトル(x, y, z)との組合わせにより回転の変換が定まります。上記に引用した[ヘルプ]の「四元数表記」の説明と、まさに符合します。

これに対して四元数は、4つの元(値)の組でひとつの回転を表します。回転の軸となる3次元の単位ベクトルをU = (x, y, z)とするとき、角度θの回転はつぎのような四元数Qで表されます。なお、四元数を表す式のセミコロン(;)で区切られた左の実数の項を「スカラー部」、右の3次元ベクトル(U)が含まれる項を「ベクトル部」といいます。

Q = (cos(θ/2); sin(θ/2)U)

四元数の定義や具体的な計算については、「四元数(クォータニオン)」をお読みください。ここでは、回転軸を表す3次元ベクトルUにも、角度に関わる三角関数sin(θ/2)が掛合わせられていることに着目すれば充分です。つまり、3次元ベクトルUも、角度を定めるためにひと役買っていることを意味するからです。

軸角度と比べるために、四元数にもとづく回転の情報を確かめてみましょう。y軸つまり単位ベクトルU_y = (0, 1, 0)を回転の軸として、60度(π/3ラジアン)回転するフレームアクションを試します(スクリプト002)。なお、y軸を表す単位ベクトルは、定数Vector3D.Y_AXISとして備わっています。

スクリプト002■y軸の単位ベクトルで回転して四元数の情報を得る

var myMatrix3D:Matrix3D = new Matrix3D();
myMatrix3D.prependRotation(60, Vector3D.Y_AXIS);
var quaternion:Vector3D = myMatrix3D.decompose(Orientation3D.QUATERNION)[1];
trace(quaternion.w, quaternion);

上記スクリプト002は、Matrix3D.decompose()メソッドの第1引数に定数Orientation3D.QUATERNIONを指定しました。この[出力]は、つぎのようになります。

0.8660253882408142 Vector3D(0, 0.4999999701976776, 0)

0.866…はcos30°、0.5はsin30°になります。つまり、この回転を表す四元数がQだとすると、Vector3D.wプロパティの値がスカラー部、Vector3Dオブジェクトのプロパティ(x, y, z)の表す3次元ベクトルがベクトル部を示しているのです。

Q = (cos(60°/2); sin(60°/2)U_y)
= (cos30°; sin30°(0, 1, 0))
= (cos30°; (0, sin30°, 0))
= (0.866, (0, 0.5, 0))

F-site

[AS3] Vector3Dの四元数表現 [Edit]

この記事へのコメント